Preamble

SDP is the university third year Computer Science system design project. The task is to build and develop a robot to play two-a-side football loosely based on the rules of the RoboCup SSL. Teams have twelve members in two groups of six, one per robot. The system architecture, at an abstract level, is comprised of a vision system, strategy AI/planner, computer-to-robot communications module and of course the robot's hardware and firmware.

Project Documents

Specification Specification

User-Guide User-Guide

GitHub repo GitHub repo

Arduino.ino

To ensure reliable motion multiple commands were sent until one was recieved. The checksum ensures that the command bits were all correct and prevents the repition of any single command.


/* Returns true if the command should be ignored in case
 * it is a duplicate command or bad checksum */
bool ignore() {  
  int seqNo = atoi(sc.next());
  if (seqNo == lastSeqNo) {
    done();
    return true;
  }
  
  int checksum = atoi(sc.next());
  
  int sum = 0;
  paramCount = 0;
  while (char *token = sc.next()) {
    params[paramCount] = atoi(token);
    sum += abs(params[paramCount]);
    ++paramCount;
  }
  if (checksum != sum) {
    Serial.print(RESP_ERROR_CHECKSUM);
    return true;
  }
  
  done();
  lastSeqNo = seqNo;
  return false;
}

Moving in any direction

The motion was constructed by calculating the angle between the desired direction and the robot's orientation $x$ . The angle was then rotated by 45 degrees as our robots front sat directly between two wheels. This was used to compute the driving components that were sent to the Arduino. The matrix multiplication below was used to extract the driving powers and then each power was scaled up by a factor of 100 divided by the absolute maximum of the four motor powers so that the robot was always at max speed.

\[\begin{pmatrix} \text{MOTOR 0}\\ \text{MOTOR 1}\\ \text{MOTOR 2}\\ \text{MOTOR 3} \end{pmatrix} = \begin{pmatrix} 1 & 0\\ 0 & -1\\ -1 & 0\\ 0 & 1 \end{pmatrix} \begin{pmatrix} \cos(45-x)\\ \sin(45-x) \end{pmatrix} \]

Staying out of the penalty box

We deceided to use a planner based of potential field charges. An infinite line charge was used to simulate a repulsive pitch marking such as off side and the opponents penalty box.

\[ step = (\hat{obstacle_{\perp}})\cdot(\hat{r_{robot}} - \hat{r_{potential}}) \]

Where $\hat{obstacle_{\perp}}$ is perpendicular to the pitch marking and pointing towards the area of allowed play.
$step > 0$ excert a repulsive force, your outside of the box
$step < 0$ excert an attractive force, your inside the box

Responsive position planning

Finite line charges we're used to plan motions which correspond to the exact shortest path to an arbitary line from any position on the pitch. To calculate this, the coordinate system was rotated so that the line charge in question was flush with the x-axis using a rotation matrix.

\[ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \]

Once rotated, the perpendicular distance is simply the difference in y and position parallel to the line charge (-a to one end and b to the other) the difference in x with each end. Once the force was calculated the vector was rotated back into the original space and applied to the robot. The code below returns the direction of the resultant force.


    def get_force(position):
        angle = math.atan2(direction_vector[0],  direction_vector[1])
        start_field = rotate_vector(-angle, start_vector)
        end_field = rotate_vector(-angle, end_vector)
	rotated_point = rotate_vector(-angle, position)

        if start_field[0] > end_field[0]:
            right_ref = start_field[0]
            left_ref = end_field[0]
        else:
            left_ref = start_field[0]
            right_ref = end_field[0]

        a = rotated_point[0]-left_ref
        b = right_ref - rotated_point[0]
        d = rotated_point[1] - start_field[1]
        if d != 0 and ( a != 0 or b != 0):
	    factor1 = np.power(1/(np.power(a, 2) + np.power(d, 2)), 0.5)
            factor2 = np.power(1/(np.power(b, 2) + np.power(d, 2)), 0.5)
            outx = constant*(-factor1 + factor2)
            outy = (constant/d)*(a*factor1 + b*factor2)
            return  rotate_vector(angle,(outx,outy))
        else:
            return 0, 0

For defensive planning, we used two fixed points and created an attractive line charge between them. The robot would defend a pass by being attacted to the imaginary line.

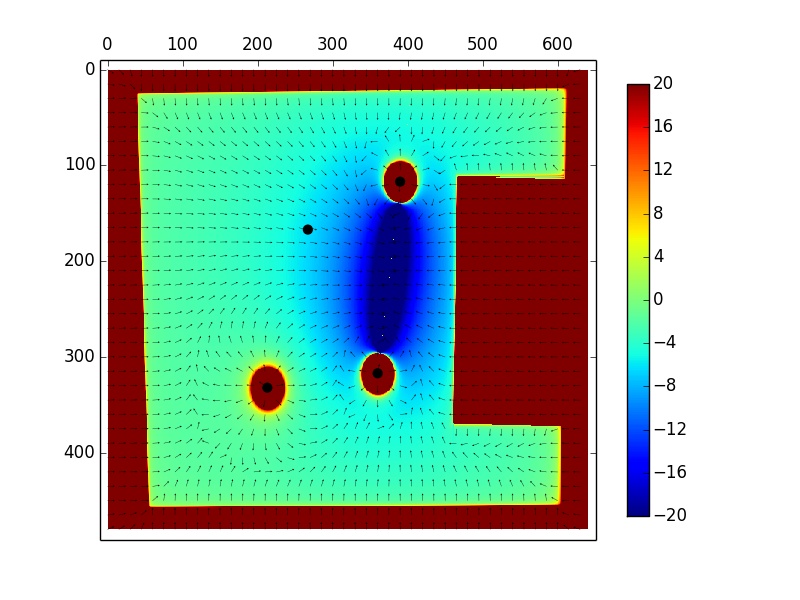
For simulating the idea of "finding space" , we created several shadowed areas caused by the opponents defense of the goal or a pass and added a repulsive line charge from the start of the shadow to a pitch length's away. The type of shadow created by each player was decided on depending on there current closest defensive position. This enabled the robot to not only get onto space but make a run around the players if the new area was a better position to play.


end_vector = start_vector[0] + normalize(direction_vector)[0]*PITCH_LENGTH,  start_vector[1] + normalize(direction_vector)[1]*PITCH_LENGTH

System Design Project